Welcome to the home of Levelology, we seek a balance and understanding.
Simplification is the key to understanding
Advanced Simplicity
Is the logical process of breaking things down to it's base constituent parts or First Principles. These fundamental building blocks
can then be examined, identities checked and verified - free from inconsistency and contradiction to the mind
for use as foundational understandings to then build upon.
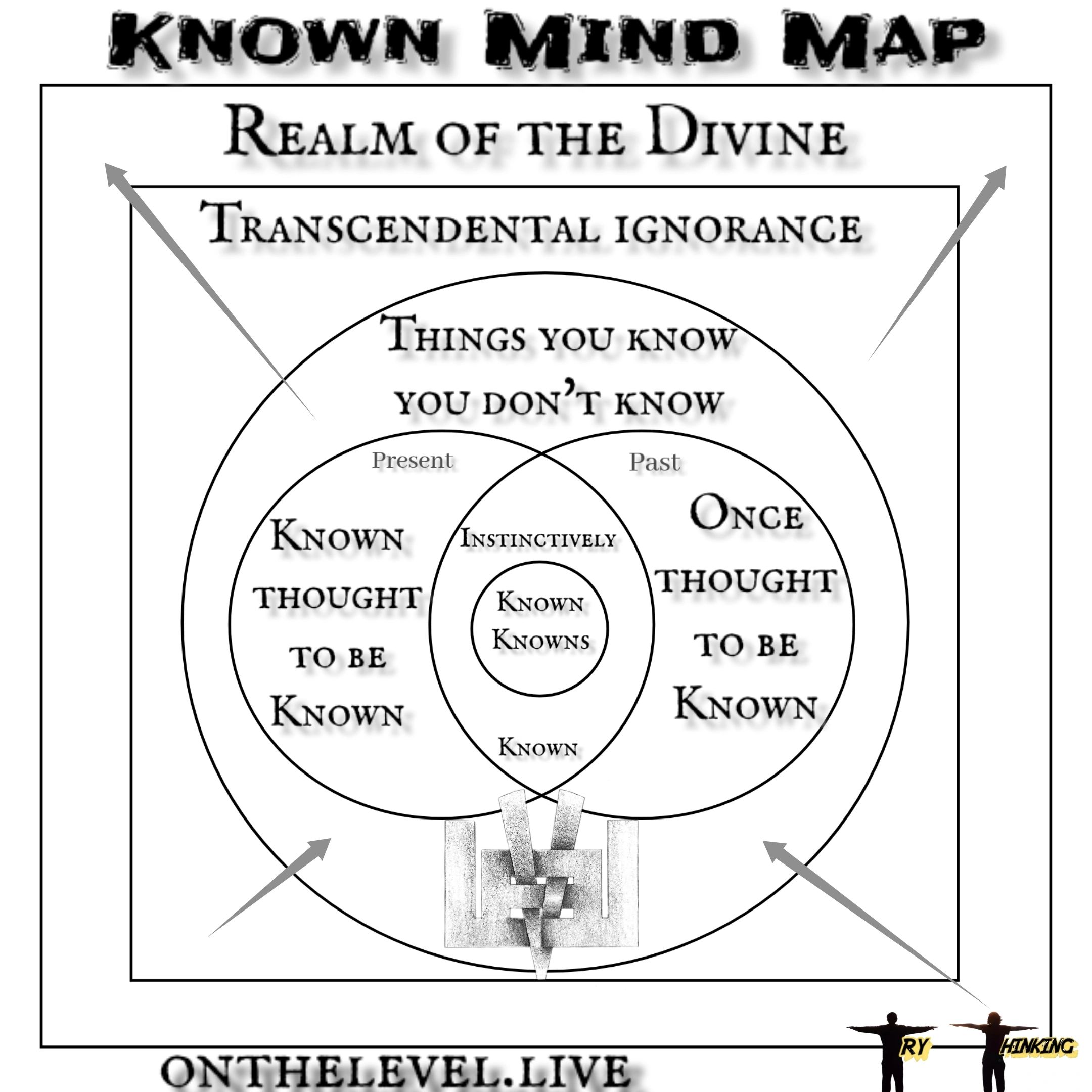
Simple to the mind.
The Truth cannot contradict itself!!!
Bev Try Thinking
The form of argument
The Modes of Argumentation
For a well rounded rhetoric these are the modes of arguments used with a brief description of how they work. Mind your P's and Q's on the first 2 and your foundations are set.
The Lemma
Not really an argument but worthy of note as it's the thing that ties the arguments toge From the Ancient Greece, λῆμμα, (perfect passive εἴλημμαι) something received or taken. Thus something taken for granted in an argument.
The Lemma is a stepping stone within argumentation to help you reach your goal.
Modus Ponens
Also known as Modus ponendo ponens (Latin - 'method of putting by placing'). Very closely linked to Modus tollens as these forms can be traced back to antiquity. In this form we affirm the P statement to affirm the Q statement, Mind your P's and Q's has never been so important as here.
If P then Q - Affirm P is true therefore Q must also be true.
Modus Tollens
Also known as Modus tollendo tollens (latin - the way that denies by denying). This is a simple form of argumentation where you deny the consequent to deny the antecedent. This is one of the most elementary (valid) logical inferences.
If P Then Q - Not Q therefore Not P.
The Transitive Law of Equality
The transitive law of equality is best known as the first axiom within Euclids Elements where he stated "Things which are equal to the same thing are equal to each other" or more commonly known as " If A equals B and B equals C, then A equals C"
Quod Erat Demonstrandum Q.E.D.
Meaning "that which was to be demonstrated". Literally it states "what was to be shown".
Reductio Ad Absurdum
In my opinion the most enjoyable mode of argumentation that seeks to establish the stupidity of a contention by showing the absurdity of the outcome, were the ridiculous contention true. Remember it's the contention being mocked not the interlocutor.
Stolen concept
This to me is the most enjoyable type of argument that can be made present day, it relies on the ignorance of the person hearing the argument and quite often the ignorance of the person presenting the argument. This type of sophistication requires a falsification in conclusion of one of the premises the argument relies on - a self refuting argument. A masterpiece in sophistical thought
A high level of sophistry is required to invent these type of argument but in present day all they need to be is scripted rhetoric, little to no understanding of the structure or validity is required due to the low functioning logic models of most people.
The Paradox
The ultimate argument - no solution, a never ending problem. This is where logos helps you meet god.
Take this argument on only if you have a safety net for you mind.
Read the quote below and take heed.
The test of a first-rate intelligence is the ability to hold two opposed ideas in the mind at the same time, and still retain the ability to function. — F. Scott Fitzgerald
Logic is self proving
On The Lemma
The Lemma is the link between the arguments, it allows you to connect the pieces.
Like reasoning, it doesn't exist by itself but it becomes the neural link between the individual arguments, that helps the mind stay on track. It's more akin to numerical mathematical operations, you can't just start of at Q without explaining how you got there. The Lemma is just that, a minor stepping stone for you to get closer to you goal. This is how at On The Level use the Lemma.
Get in Touch
Interested in learning more about how we can support your child? Contact us today to schedule a consultation.
Modus Ponens
The Argument
The Argument was wrote to link the foundations of geometry (deductive logic) to the real world to help provide a solid argument to support our understanding of reality.
I once read that if you include geometric aspects into an argument then your argument would become deductive, meaning that the argument would instantly become either provably true, or provably false.
The ALL statement was included to help show that this occurrence of ALL horizontals being parallel to the plane of the horizon happens everywhere, no matter where you are, or at any elevation.
Horizontal is an orientation, it is not just a line on a piece of paper
The Observed Phenomena
A precursor to the formulation of any argument is an observed natural phenomena that begins the process, but this observation also relies on a level of understanding in order to form the idea of the argument.
Below is a link to better explain this
Modus tollens
If the earth is flat
These 2 simple modus tollens show that a false dichotomy exists when given only these 2 options. The modus tollens is useful in disproving the claims made by everyday people in everyday life about everyday things.
Finding these contradictions and false dichotomies all around us can be troublesome to the mind.
If the earth is a spherical object
Knowing of the false dichotomy gives you chance to realise the shear scale of the dogma that exists all around us.
Inclusive Special Education Services
The transitive law of equality
Euclid chose this as his first Axiom - Things which are equal to the same thing are equal to one another, or If A=B and B=C then A=C, A=B Λ B=C ⊃ A=C
Get in Touch
Interested in learning more about how we can support your child? Contact us today to schedule a consultation.
Inclusive Special Education Services
The transitive law of equality
Euclid chose this as his first Axiom - Things which are equal to the same thing are equal to one another, or If A=B and B=C then A=C, A=B Λ B=C ⊃ A=C
Get in Touch
Interested in learning more about how we can support your child? Contact us today to schedule a consultation.